Symbol Crash

不学无术

0%

基础密码知识

发表于 更新于 分类于
本文字数： 2.6k 阅读时长 ≈ 10 分钟

常见加密模式

为什么要分模式？

对称加密算法（如AES）只能加密固定长度的数据块（比如 AES 的块是 128 位）。如果要加密一个很长的文件，就需要将文件切分成多个块，再逐个加密。

问题来了：如何让这些块之间产生关联，避免被破解？这就是加密模式的作用！

1. ECB模式（电子密码本）

  • 原理：

    • 把数据切成块，每块独立加密，像查字典一样（比如“A”对应“X”，“B”对应“Y”）。
    • 致命缺陷：相同的明文块会生成相同的密文块。

  • 例子：

    • 加密一张纯色图片（比如全黑），ECB加密后仍能看到轮廓（如下图）。

    • 加密“HelloHello”，两个“Hello”块加密后完全一样。

      ECB模式问题

结论：永远不要用ECB，除非加密单个块（比如一个密码）。

2. CBC模式（密码块链）

  • 原理：

    1. 初始化向量（IV）：在加密第一个块前，生成一个随机数（IV），与第一个明文块做异或（XOR）。
    2. 链式反应：每个明文块加密前，先与前一个密文块做XOR，再加密。

  • 例子：

    • 加密“Hello”：

      • 生成IV（比如“随机数123”），与“Hello”做XOR，再加密。
      • 第二个块“World”先与第一个块的密文做XOR，再加密。

    • 即使两个明文块相同，加密后的结果也不同。

  • 优点：：安全性高，适合文件加密。

  • 缺点：

    • 需要存储或传输IV（通常明文传输，无需保密）。
    • 无法并行加密（必须按顺序处理块）。

3. CTR模式（计数器模式）

  • 原理：

    1. 生成一个计数器（比如从0开始递增：0,1,2,3…）。
    2. 加密计数器，得到一个密钥流（伪随机数）。
    3. 将密钥流与明文块做XOR，得到密文。

  • 例子：

    • 加密“Hello”：
      • 加密计数器0得到密钥流“X3k%”，与“Hello”XOR得到密文。
      • 加密计数器1得到密钥流“aB9$”，与下一个块XOR。

  • 优点：

    • 支持并行加密和解密（因为不依赖前一个块）。

    • 可以实时加密（比如视频流）。

  • 缺点：

    • 计数器不能重复（否则安全性崩溃）。

4. GCM模式（伽罗瓦计数器模式）

  • 原理：
    结合CTR模式的高效性，并附加认证标签（MAC），验证数据是否被篡改。

  • 例子：

    • 加密一段消息后，生成一个“指纹”（比如“d8e9f”）。

    • 接收方解密时验证指纹，如果指纹不匹配，说明数据被篡改。

  • 优点：

    • 加密+认证一步完成（适合网络传输，如HTTPS）。
    • 高效且安全。

  • 缺点：

    • 实现复杂，需要处理计数器溢出问题。

5. CFB/OFB模式（反馈模式）

  • 原理：

    • 类似于CTR，但生成密钥流的方式不同。
    • CFB（密码反馈）：将前一个密文块加密后生成密钥流。
    • OFB（输出反馈）：将前一个密钥流加密后生成新的密钥流。

  • 用途：

    • 适合流数据（如实时语音），但现代应用更倾向用CTR或GCM。

加密模式对比表

模式 安全性 速度 并行性 适用场景
ECB ❌ 低 ⚡快 ✔️ 支持 已淘汰（仅用于单块加密）
CBC ✔️ 高 🐢 慢 ❌ 不支持 文件加密（需顺序处理）
CTR ✔️ 高 ⚡快 ✔️ 支持 实时数据流（视频、网络传输）
GCM ✔️ 超高 ⚡快 ✔️ 支持 需要认证的传输（HTTPS、VPN）
CFB ✔️ 中 🐢 慢 ❌ 不支持 遗留系统（逐渐被取代）

ECB 是“独狼”，CBC是“链条”，CTR是“流水线”，GCM是“保镖+流水线”

常见对称加密算法

算法 加密模式 密钥长度 应用 优点 缺点
AES (Advanced Encryption Standard) ECB, CBC, CTR, GCM, OFB, CFB 128, 192, 256位 数据加密、文件加密、通信加密等 安全性高，支持多种加密模式，广泛使用 对于某些模式（如ECB）存在模式相关的安全问题
DES (Data Encryption Standard) ECB, CBC, OFB, CFB, CTR 56位 曾用于早期的加密系统 计算速度快，硬件支持广泛 密钥长度过短，已不再安全
3DES (Triple DES) ECB, CBC, OFB, CFB 112位或168位 用于替代DES的系统，金融领域等 提供比DES更强的安全性 效率较低，逐渐被AES替代
Blowfish ECB, CBC, OFB, CFB, CTR 32位到448位 用于文件加密、VPN、硬盘加密等 密钥长度灵活，速度较快，简单高效 密钥管理不如AES，存在某些漏洞
RC4 流加密模式（Stream Cipher） 40位到2048位 WEP加密、SSL/TLS协议等 实现简单，速度较快 存在已知安全漏洞，逐步被淘汰
Twofish ECB, CBC, OFB, CFB, CTR 128位、192位、256位 用于加密文件、通信协议、硬盘加密等 安全性高，灵活的密钥长度，设计简洁 相较于AES，使用较少，支持硬件加速较少

常见密钥协商算法

算法 原理 应用 优点 缺点
Diffie-Hellman (DH) 基于离散对数问题，允许双方在公开通道上协商出共享密钥。 广泛用于TLS/SSL协议。 安全性较高，理论上不易被破解。 容易受到中间人攻击（MITM），缺乏身份认证。
Elliptic Curve DH (ECDH) 使用椭圆曲线数学结构，提供与DH相同的安全性，但密钥尺寸更小。 现代加密协议，如TLS、VPN等。 高效、适合资源有限的设备。 需要更高的数学理解和实现复杂度。
RSA 基于大整数分解问题，使用接收方的公钥加密会话密钥，接收方使用私钥解密。 传统的TLS/SSL协议，数字签名等。 安全性较高，已广泛应用。 加密效率较低，缺乏前向保密性，密钥较大。
Quantum Key Distribution (QKD) 利用量子力学原理（量子纠缠、量子叠加）确保密钥交换的安全性。 未来的量子计算环境中的密钥交换。 极高的安全性，即使量子计算机出现也能保证安全。 目前技术不成熟，基础设施复杂且成本高。
Post-Quantum Cryptography (PQC) 针对量子计算攻击的加密算法，确保在量子计算机时代仍然安全。 量子计算发展后的加密解决方案。 为未来量子计算带来的威胁提供抗性。 当前实现不成熟，标准尚在制定中。
Kerberos 基于对称密钥的认证协议，使用中心认证服务器（KDC）进行身份验证和密钥分发。 企业环境中网络身份验证。 提供安全的身份验证，支持单点登录（SSO）。 需要配置复杂的KDC基础设施。
Secure Remote Password (SRP) 基于密码的认证协议，避免密码直接传输，双方使用共享密钥进行加密通信。 基于密码的应用，如安全远程登录。 提供无密码传输的安全验证，适合基于密码的应用。 实现复杂，性能上相对较差。

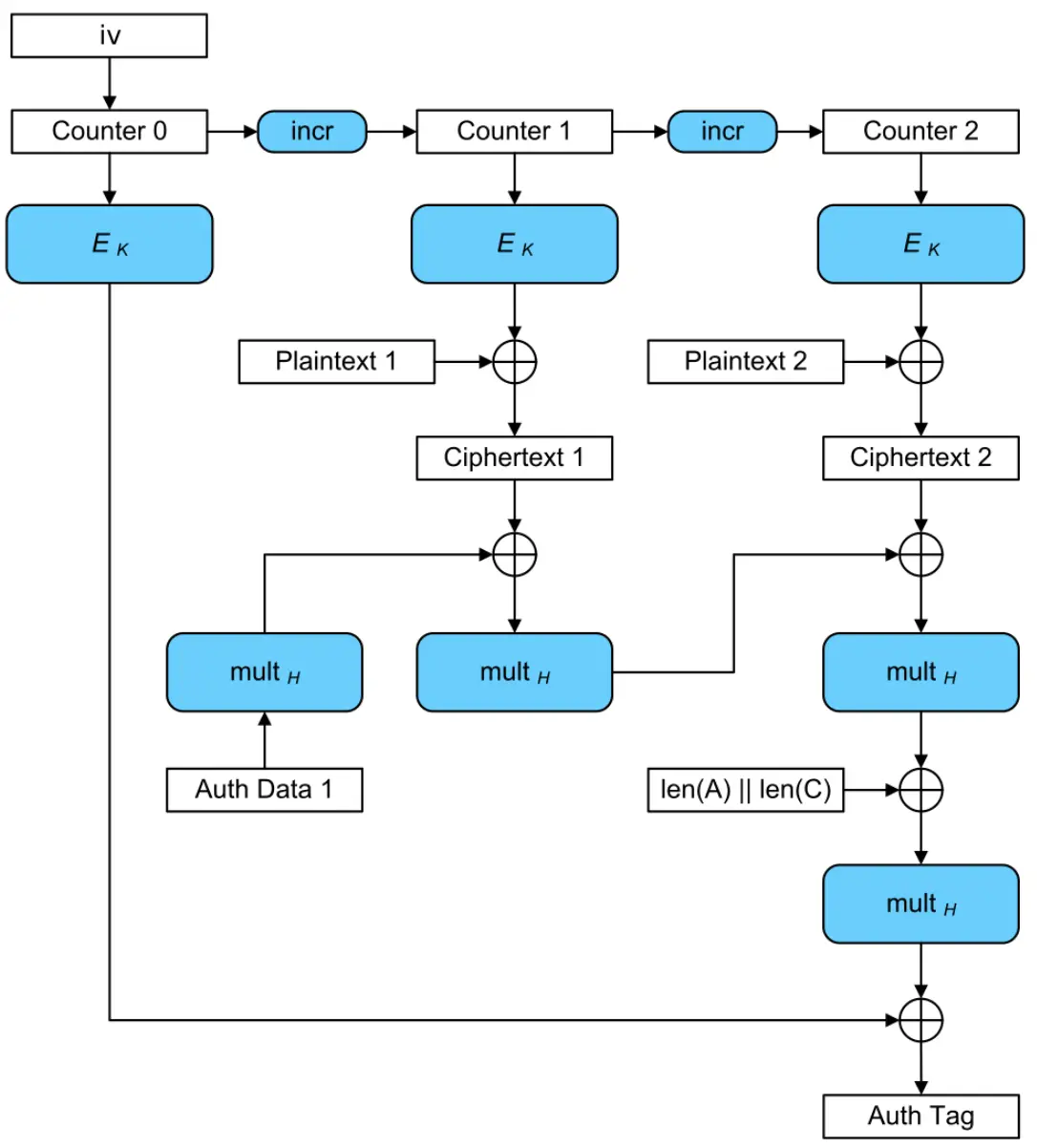
AES-GCM

AES-GCM（Advanced Encryption Standard - Galois/Counter Mode）是一种结合加密和认证的对称加密模式，广泛应用于需要高效保密性和数据完整性的场景（如TLS、IPSec）。以下是其核心步骤的详细分解：

1. 参数初始化

  • 密钥（Key）：128/192/256位的 AES 密钥，用于加密和生成认证标签。
  • 初始向量（IV）：通常为 12 字节（推荐长度），需全局唯一，避免重复。
  • 附加认证数据（AAD）：可选明文数据，参与认证但不加密。
  • 明文（Plaintext）：待加密的数据。

2. 生成初始计数器块（J₀）

  • IV 处理：
    • 若 IV 为 12 字节：直接作为前 12 字节，后接4字节计数器（0x00000001），组成 16 字节的 $J_0$ 。
    • 若 IV 非 12 字节：通过 GHASH 计算生成 $J_0$（见步骤6）。

3. 加密过程（CTR模式）

  • 生成密钥流：

    • 初始计数器块：$J_0$ 的31位最低有效位（LSB）递增，生成计数器序列 J₀+1, J₀+2, ...。
    • 对每个计数器块进行 AES 加密，生成密钥流块。

  • 生成密文：

    • 明文分块（每块16字节）与对应密钥流异或，得到密文。

4. 认证过程（GHASH）

GHASH 核心操作：在 Galois 域 $\mathrm{GF}(2^{128})$ 上的乘法，使用哈希子密钥 $H$,（由加密全0块得到, $H = \mathrm{AES\text{-}Encrypt}(\mathrm{Key}, \mathbf{0}^{128})$）。

步骤：

  1. 处理AAD：

    • 将 AAD 填充为 16 字节的倍数，不够补零，分块为 $A_1, A_2, \ldots, A_m$。
    • 计算 GHASH：初始为X = 0（128位全0），依次与 AAD 块异或后乘 $H$。

    $$
    X = (X \oplus A_i) \otimes H
    $$

  2. 处理密文：

    • 将密文填充为 16 字节的倍数，不够补零，分块为 $C_1, C_2, \ldots, C_m$。
    • 继续 GHASH 计算，与密文块异或后乘 $H$。

    $$
    X = (X \oplus C_i) \otimes H
    $$

  3. 处理长度块：

    • 拼接 AAD 长度和密文长度（各64位），组成 16 字节块。

      • （1）单位必须为比特（bit）
      • （2）64 位无符号整数表示
      • （3）前 8 字节为 AAD 长度，后 8 字节为密文长度 的顺序拼接

    • 最后与长度块异或后乘 $H$，得到 GHASH 输出 $S$ 。

    $$
    \begin{aligned}
    \text{Len} &= \text{len}(\text{AAD})\ \texttt{||} \ \text{len}(\text{Ciphertext}) \\
    S &= (X \oplus \text{Len}) \otimes H
    \end{aligned}
    $$

📘 符号说明：

  • $\texttt{||}$ 表示拼接（concatenation）
  • $\oplus$ 表示异或（XOR）
  • $\otimes$ 表示伽罗瓦域乘法（$\mathrm{GF}(2^{128})$）
  • len(...) 表示比特长度，通常为 64 位整数（如 GCM 中的定义）
  • X 是前一轮 GHASH 累加值
  • H 是 GHASH 中的密钥（通常由 AES 加密 0 块得出）

5. 生成认证标签（Tag）

  • 加密 $J_0$：$T = \mathrm{AES\text{-}Encrypt}(J_0) \oplus S$
  • 截断 T 为指定长度（通常16字节）作为最终认证标签。

6. 输出结果

  • 密文（Ciphertext）：加密后的数据。
  • 认证标签（Tag）：用于验证数据完整性和真实性的签名。

安全注意事项

  • IV 唯一性：重复IV会导致密钥流复用，破坏安全性。
  • 密钥管理：定期更换密钥，避免泄露。
  • 认证失败处理：标签验证失败时需丢弃数据，防止篡改攻击。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
+---------------------+
| 初始化参数           |
| - Key               |
| - IV                |
| - AAD               |
| - Plaintext         |
+---------------------+
          |
          v
+---------------------+
| 生成初始计数器块 J₀  | → 若IV=12字节: J₀ = IV || 0x00000001
|                     | → 否则: J₀ = GHASH(IV)
+---------------------+
          |
          v
+---------------------+       +---------------------+
| CTR模式加密          |       | GHASH认证过程       |
| 1. J₀+1, J₀+2,...    |       | 1. 计算H = AES(0)   |
| 2. 生成密钥流        |       | 2. 处理AAD → X      |
| 3. 明文异或密钥流 → 密文 |   | 3. 处理密文 → X     |
|                     |       | 4. 处理长度块 → S    |
+---------------------+       +---------------------+
          |                             |
          |                             v
          +------------+  +-------------+
                       |  |
                       v  v
+---------------------+
| 生成认证标签         |
| T = AES(J₀) ⊕ S      |
| 截断T为Tag           |
+---------------------+
          |
          v
+---------------------+
| 输出结果             |
| - 密文               |
| - Tag               |
+---------------------+

aes-gcm-diagram